.jpg)
Sistemas Acústicos
Consideremos ahora que se desea estudiar el movimiento de una masa de aire de densidad ρ, contenido en una columna de sección S y longitud infinitesimal. Antes de iniciarse el desplazamiento de las moléculas de aire, al producirse una perturbación, el aire se encuentra en reposo, aunque las partículas tengan un movimiento al azar, pero no existe movimiento del aire en ninguna dirección, por lo que el desplazamiento de las partículas es cero, luego su velocidad vibratoria también será cero, o sea al no existir ninguna perturbación en el medio la presión será constante en toda su extensión, de valor P0 el volumen ocupado V0 y la densidad ρ0. Se sabe que toda fuerza que tiende a comprimir un gas, produce necesariamente un desplazamiento de sus partículas. Los valores definidos en el equilibrio, una vez que se perturba el aire, sufriendo una compresión (alta presión) o un enrarecimiento (baja presión), se verán modificados (figura 1.11).
1- La presión P0 varía a P = P0 + p siendo p la variación de presión.
2- El volumen V0 varía a V = V0 + X siendo X la variación de volumen.
3- La densidad ρ0 varía a ρ1 = ρ0 + ρ siendo ρ la variación de densidad.
 |
| Moléculas desplazadas por vibración creadas de a) pequeña amplitud, b) de gran amplitud. Figura 1.11. |
a) Oscilación libre sin pérdidas
Un sistema formado por una masa de aire, que tiene elasticidad, si se produce una presión incremental en el aire, esta es directamente proporcional a una variación incremental del volumen.
La ecuación de movimiento de las moléculas del aire, en este tipo de sistema, depende del módulo de compresibilidad del aire B, que caracteriza su elasticidad, así como de la masa de aire desplazada.
En los sistemas acústicos a la masa se le suele llamar inertancia, siendo el elemento que se opone a una variación del flujo de velocidad. La capacidad acústica se denomina compliancia acústica, representando el elemento que se opone a una variación de la presión sonora, o sea se define como la variación de volumen que se produce al aplicarle la unidad de presión.
b) Oscilación libre con pérdidas
El sistema acústico con masa, elasticidad y resistencia, es el denominado resonador de Helmholtz (figura 1.12). Según se puede apreciar este sistema está formado por una cavidad rígida del volumen V, que está comunicada con el medio externo a través de un pequeño cuello de radio r y longitud l, siendo S el área de la sección transversal del cuello. El aire en el cuello puede considerarse que se mueve como una unidad, de tal forma que suministra el elemento de masa del sistema.
 |
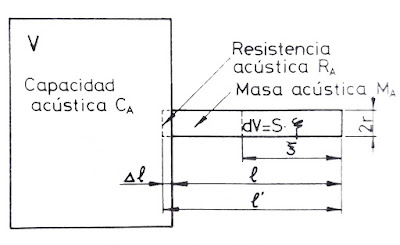| Resonador de Helmholtz. Figura 1.12. |
La presión del aire en la cavidad del resonador cambia alternativamente, siendo una compresión y una expansión, debido al flujo de aire que atraviesa el cuello, haciendo que la presión aumente (compresión) y seguidamente disminuya (expansión), por lo que el volumen de gas de la cavidad actúa como un resorte. El elemento resistivo del sistema, despreciando las fuerzas de viscosidad, se debe a la radiación de la perturbación en la abertura, disipándose en forma de energía.
La ecuación del movimiento de las oscilaciones propias amortiguadas en el aire, dependerá de los parámetros característicos del resonador de Helmholtz, así como de la frecuencia angular de la perturbación, del número de onda k - (k = 2 π / λ), siendo λ (longitud de onda) el espacio recorrido por la oscilación en un tiempo igual a un período.
c) Oscilaciones forzadas con amortiguamiento
Si al sistema acústico descrito anteriormente, se le somete continuamente a una presión de tipo alterno, la ecuación de movimiento se verá modificada por esta nueva fuerza. En los sistemas acústicos la magnitud que se puede medir con más facilidad, sin modificación del circuito, es la presión acústica p, que es el exceso de presión que existe en un punto de un medio, con relación a la presión en equilibrio existente en dicho medio (p = Δ P = P - P0 N/m 2), siendo uno de los parámetros en este tipo de sistemas. Otro parámetro es la velocidad de volumen U, que es el volumen de fluido desplazado en un segundo.
De forma análoga a los sistemas estudiados anteriormente, la ecuación de su dinámica depende de los parámetros característicos del sistema.
La impedancia acústica ZA a la entrada del resonador, se define como el cociente entre la presión acústica supuesta uniforme sobre toda la superficie, y la velocidad de volumen, o flujo a través de esta superficie, su unidad es el ohmio acústico (kg/m⁴ .S).
Existen tres definiciones diferentes de impedancia acústica:
1- "Impedancia acústica específica" Z = p/v, que es una propiedad característica del medio y del tipo de ondas que se propagan a través del mismo, esta definición es útil para estudiar ondas acústicas que pasan de un medio a otro. Luego la impedancia acústica específica se define para un punto del medio, al dar el valor tanto de la presión acústica, como de la velocidad de la partícula en el mismo punto.
2- "Impedancia acústica'" ZA = p/U, se usa para estudiar problemas de radiación de superficies vibrantes, siendo ZA = Z/S.
3- "Impedancia de radiación" Zr = F/v, se emplea para estudiar la relación entre las ondas acústicas y las fuentes que las producen. La relación existente entre esta impedancia y las dos expuestas anteriormente es, Zr =Z• S y Zr = ZA• S².
En los sistemas acústicos, la frecuencia de resonancia, es aquella para la que la reactancia acústica se anula, dependiendo de una constante c característica del aire, así como de la relación S/l' donde S es el área de la abertura y l' la longitud efectiva de la abertura, llamando a la relación S/l' conductividad de la abertura, y del volumen de la cavidad V,
Manuel Recuero López
.jpg)