Desentrañando los Modos Propios (Modos Acústicos): La Huella Resonante de tu Sala
Cuando el sonido se encuentra confinado dentro de un espacio cerrado, como una habitación o un estudio, su comportamiento se ve profundamente influenciado por las dimensiones de ese espacio. Las ondas sonoras reflejadas interactúan entre sí, dando lugar a fenómenos de interferencia constructiva y destructiva a frecuencias específicas. Estas frecuencias de resonancia inherentes a la sala se conocen como modos propios o modos acústicos, y comprenderlos es fundamental para lograr un sonido preciso y controlado en cualquier entorno de escucha o producción. Al final de esta entrada encontrarás un Excel para calcular los Modos Propios de tu propia Sala.
El Nacimiento de las Ondas Estacionarias: La Base de los Modos Propios
Imagina un altavoz emitiendo un tono puro (una única frecuencia) en una habitación. Las ondas sonoras irradian en todas direcciones y se reflejan en las paredes, el suelo y el techo. Parte de este sonido reflejado regresa a la fuente (o a cualquier otro punto de la sala). Si la distancia recorrida por la onda reflejada es un múltiplo entero de la longitud de onda del tono, la onda reflejada estará en fase con la onda incidente, sumándose y reforzando esa frecuencia específica. Este fenómeno da origen a una onda estacionaria, que es la manifestación física de un modo propio de la sala para esa frecuencia particular.
Además de la frecuencia fundamental de un modo propio, cualquier múltiplo entero de esa frecuencia también generará una onda estacionaria y, por lo tanto, otro modo propio. Esto ocurre porque sus longitudes de onda más cortas también "encajarán" en el recorrido de la onda reflejada, llegando en el segundo, tercer o siguiente ciclo de la onda original. Este concepto está íntimamente ligado a nuestra comprensión de la "Frecuencia y su Respuesta: Entendiendo las Ondas Sonoras".
 |
| Figura 1: Representación gráfica de un tono puro de 1000 Hz en el dominio del tiempo y la frecuencia. |
La Figura 1 muestra una sinusoide simple en el tiempo y un único pico en el espectro de frecuencias a 1000 Hz, ilustrando la naturaleza de un tono puro utilizado para excitar los modos propios.
La Tríada de los Modos: Axiales, Tangenciales y Oblicuos
Los modos propios se clasifican en tres tipos, dependiendo del número de superficies paralelas entre las que se forman las ondas estacionarias:
- Modos Axiales: Se generan entre dos superficies paralelas opuestas (por ejemplo, pared frontal-pared trasera, pared lateral-pared lateral, suelo-techo). Estos son los modos más energéticos, ya que la onda sufre menos pérdidas por reflexión.
- Modos Tangenciales: Resultan de las reflexiones en cuatro superficies (por ejemplo, dos paredes laterales, el suelo y el techo). Estos modos tienen aproximadamente la mitad de la energía de los axiales (-3 dB por cada reflexión adicional).
- Modos Oblicuos: Se forman por las reflexiones en las seis superficies de la sala (las cuatro paredes, el suelo y el techo). Son los modos con menor energía, con una atenuación adicional de aproximadamente 6 dB en comparación con los axiales.
La Figura 2 muestra una sala rectangular con líneas representando las ondas estacionarias fundamentales axiales para el largo, ancho y alto, indicando los puntos de máxima presión (antinodos) en las paredes y los puntos de mínima presión (nodos) entre ellas. Esta figura podría hacer referencia a nuestra entrada sobre "Ondas Estacionarias, Respuesta en Graves y Medidas de Sala", donde exploramos en detalle la formación de nodos y antinodos.
El Espectro Modal: Una Huella Acústica Única
Cuando se reproduce un programa de audio complejo, con una amplia gama de frecuencias, se excita simultáneamente un gran número de modos propios dentro de la sala. El conjunto de todas estas ondas estacionarias define el espectro modal del recinto, una especie de "huella acústica" única para cada sala. La presencia de estos modos provoca una coloración del espectro sonoro, ya que las frecuencias que coinciden con los modos propios son reforzadas (en los antinodos), mientras que otras frecuencias pueden sufrir cancelaciones (en los nodos).
Además de la coloración espectral, los modos propios generan variaciones significativas en la presión sonora en diferentes ubicaciones dentro de la sala. En los límites del recinto (las paredes, el suelo y el techo), siempre se encuentran antinodos (puntos de máxima amplitud o presión). Particularmente problemáticas son las esquinas, donde convergen los antinodos de los modos axiales de los tres ejes, creando acumulaciones de energía en las frecuencias resonantes. Esta acumulación de energía en las esquinas puede ser abordada con "Trampas de Graves. Hazla tu mismo".
Esta representación espacial de la respuesta en frecuencia es una de las razones por las que la "Percepción del Espacio" sonoro se ve afectada en salas con modos propios prominentes.
Calculando la Resonancia: La Fórmula de los Modos Propios
Para determinar las frecuencias de los modos propios de una sala rectangular, utilizamos la siguiente fórmula tridimensional derivada de la ecuación de onda:
Donde:
- f (nx, ny, nz ) es la frecuencia del modo propio (en Hz).
- c es la velocidad del sonido (aproximadamente 343 m/s a temperatura ambiente, aunque un valor de 340 m/s se usa a menudo para simplificar los cálculos). La velocidad del sonido varía con la temperatura según la relación c = 331.3 + 0.606⋅T (°C).
- L es el largo de la sala (en metros).
- W es el ancho de la sala (en metros).
- H es la altura de la sala (en metros).
- nx, ny, nz son números enteros no negativos (0, 1, 2, 3, ...), que representan el orden del modo a lo largo de los ejes x (ancho), y (largo) y z (alto) respectivamente.
- Para los modos axiales, uno de los valores de nx, ny o nz es 1 o mayor, mientras que los otros dos son 0. Por ejemplo, el modo axial fundamental a lo largo del largo de la sala sería f(0,1,0).
- Para los modos tangenciales, uno de los valores de nx, ny o nz es 0, mientras que los otros dos son 1 o mayores (por ejemplo, f(1,1,0).
- Para los modos oblicuos, ninguno de los valores de nx, ny o nz es 0 (por ejemplo, f(1,1,1).
Caso Práctico: Análisis de un Estudio
Consideremos una sala con dimensiones de 3.45 m (ancho), 2.90 m (largo) y 2.50 m (alto), utilizando una velocidad del sonido de 340 m/s:
Modo Axial (Ancho, nx = 1,ny = 0, nz = 0):
Modo Axial (Largo, nx = 0,ny = 1, nz = 0):
Modo Axial (Alto, nx = 0,ny = 0, nz = 1):
El cálculo de modos tangenciales y oblicuos implica combinaciones no nulas de los índices nx, ny y nz.
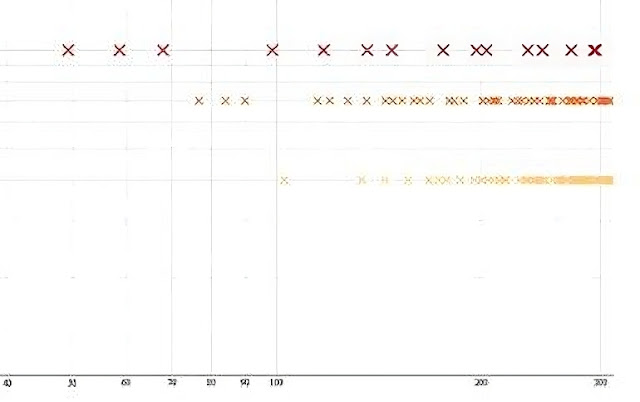 |
| Figura 3: Modos propios por debajo de 300 Hz |
Identificando los Problemas: Modos Degenerados y Huecos Modales
Al analizar el espectro modal de una sala, es crucial identificar dos problemas principales:
- Modos Degenerados: Ocurren cuando dos o más modos propios tienen la misma frecuencia o frecuencias muy cercanas. Esto provoca un refuerzo excesivo en esas frecuencias, resultando en picos resonantes muy pronunciados y una respuesta de graves desequilibrada. Las salas cúbicas (con largo = ancho = alto) son el peor escenario, ya que los tres primeros modos axiales fundamentales coinciden en frecuencia. Salas con dimensiones que son múltiplos simples entre sí también son propensas a modos degenerados.
- Huecos Modales: Son rangos de frecuencia donde hay pocos o ningún modo propio. Esto puede generar una falta de respuesta y una sensación de "vacío" en esas frecuencias.
La sala de ejemplo (3.45m x 2.90m x 2.50m) presentaba un buen espaciamiento general, pero con una posible escasez de modos entre 70 y 90 Hz y una acumulación alrededor de 295 Hz.
 |
| Figura 4: Gráfico comparando la distribución de los modos axiales en una sala cúbica (modos degenerados) y en una sala con proporciones más adecuadas (mejor espaciamiento). |
La Figura 4 se relaciona directamente con nuestra entrada sobre "Ondas Estacionarias, Respuesta en Graves y Medidas de Sala", donde discutimos la importancia de las proporciones de la sala.
El Diseño Importa: Proporciones para una Acústica Óptima
Como se destaca en la segunda entrada, la forma general de la habitación tiene un impacto significativo en su respuesta acústica. Un principio fundamental en el diseño de estudios es evitar las formas cúbicas. Un análisis de la acústica de estudios revela las ventajas de un diseño rectangular con proporciones cuidadosamente ajustadas para optimizar la distribución de los modos propios.
El objetivo al diseñar un espacio es lograr una distribución de modos lo más uniforme posible en el rango de frecuencias problemático (generalmente por debajo de la frecuencia de Schroeder). Idealmente, los modos y sus armónicos deberían estar espaciados a intervalos de no más de 20 Hz, evitando grandes huecos y la coincidencia de frecuencias.
Se han desarrollado varias "proporciones áureas" o preferidas a lo largo del tiempo, basadas en principios matemáticos y empíricos para lograr un buen espaciamiento modal. Ejemplos comunes incluyen proporciones relativas como 1:1.14:1.42. Si la altura del techo es la unidad (por ejemplo, 2.46 metros), las otras dimensiones se calcularían multiplicando esta altura por las proporciones (ancho = 2.46 * 1.14 = 2.80 metros, largo = 2.46 * 1.42 = 3.49 metros).
La frecuencia de Schroeder (fS) marca la transición donde los modos individuales comienzan a solaparse significativamente, y la respuesta de la sala tiende a ser más uniforme. Se calcula como:
Donde RT60 es el tiempo de reverberación de la sala (en segundos) y V es el volumen de la sala (en metros cúbicos). Por encima de esta frecuencia, el tratamiento acústico se centra más en la "Absorción de las Ondas Sonoras" y la "Reflexión, Refracción y Difracción de las Ondas Sonoras" para controlar la reverberación y las reflexiones tempranas (tema que también tratamos en "Reflexiones Tempranas").
 |
| Figura 5: Gráfico comparando la densidad de modos por debajo de la frecuencia de Schroeder en una sala con buenas proporciones y una con malas proporciones. |
La Figura 5 podría mostrar dos gráficos de densidad de modos en función de la frecuencia. La sala con buenas proporciones mostraría una densidad de modos más uniforme en el rango de bajas frecuencias.
Soluciones Prácticas: Tratamiento Acústico y Ubicación de Monitores
En salas existentes, donde las dimensiones no se pueden alterar fácilmente, el tratamiento acústico y la ubicación estratégica de los monitores son las principales herramientas para mitigar los problemas de los modos propios.
- Tratamiento Acústico: La colocación de "Trampas de Graves" en las esquinas y a lo largo de las paredes es fundamental para absorber la energía de las ondas estacionarias en las frecuencias resonantes. Paneles absorbentes en las paredes y el techo ayudan a controlar las reflexiones generales y pueden tener un impacto secundario en la atenuación de los modos.
- Ubicación de Monitores y Oyente: Evitar las esquinas y las paredes centrales, y experimentar con diferentes posiciones a lo largo de las paredes (siguiendo reglas como la del tercio o la proporción áurea) puede minimizar la excitación de los modos problemáticos y encontrar un punto de escucha con una respuesta en graves más equilibrada. Nuestra entrada sobre "Como colocar tus Monitores" ofrece más detalles sobre este proceso.
El Caso Práctico: The Wool Hall
El ejemplo de The Wool Hall ilustra cómo se aborda el diseño acústico en un estudio profesional. La atención a las proporciones de la sala, el uso de materiales absorbentes (trampas de graves en el techo y alrededor de los monitores), y la consideración de la ubicación de los equipos son elementos clave para crear un entorno de grabación y mezcla de alta calidad. La mención de evitar paredes paralelas como un buen punto de partida subraya la importancia de las proporciones en el control de los modos propios y las reflexiones (eco de vibración).
Conclusión: Dominando las Resonancias para un Sonido Preciso
Comprender y calcular los modos propios de una sala es un paso esencial para cualquier persona que trabaje con sonido. Ya sea diseñando un nuevo espacio o acondicionando uno existente, identificar las resonancias inherentes permite tomar decisiones informadas sobre la acústica, la ubicación de los equipos y el tratamiento necesario para lograr un sonido preciso, equilibrado y libre de coloraciones no deseadas. Dominar los modos propios es, en última instancia, dominar la base acústica de nuestro entorno sonoro.
Excel para Calcular Modos Propios








