Ondas Planas Longitudinales

El Viaje Invisible del Sonido: Ondas, Presión y la Escala de los Decibelios

El sonido, esa experiencia cotidiana que nos conecta con el mundo, es fundamentalmente una alteración de presión que se propaga a través de un medio elástico como el aire. Cuando una perturbación ocurre en un punto, no se queda confinada allí, sino que se irradia, transmitiendo su energía a las partículas circundantes en una onda progresiva. El punto de origen de esta perturbación se conoce como foco o fuente. A diferencia de una partícula que transporta su masa y energía, una onda elástica transporta energía a través de las deformaciones elásticas del medio.

Partículas oscilando en la dirección de propagación.

La Naturaleza Ondulatoria del Sonido: Inercia y Elasticidad

Para que una onda sonora se desplace a través de un medio material, este debe poseer dos propiedades esenciales: inercia y elasticidad. La inercia, relacionada con la densidad del medio (la masa por unidad de volumen), permite que una porción del medio transfiera la perturbación a sus vecinas. La elasticidad, por otro lado, genera una fuerza restauradora sobre cualquier elemento desplazado de su posición de equilibrio, impulsándolo a retornar a ella. El aire, afortunadamente, posee ambas propiedades, lo que permite la propagación del sonido.

El sonido se genera cuando el aire entra en vibración, generalmente por el contacto con un objeto vibrante. Subjetivamente, el sonido es la sensación auditiva que experimenta nuestro nervio acústico a través de los órganos del oído. Objetivamente, es el movimiento vibratorio longitudinal que da origen a esa sensación.

Consideremos una cuerda de guitarra tensa que se golpea. Vibra rápidamente, desplazándose de su posición de reposo y oscilando alrededor de ella con una amplitud decreciente hasta detenerse. Al hacerlo, la cuerda empuja y comprime el aire que tiene delante, mientras que el aire detrás se expande para llenar el vacío. Este movimiento se transmite a las capas de aire adyacentes, propagándose en todas direcciones desde la fuente como una onda.

Un cambio físico crucial asociado a la propagación de una onda sonora es la variación de la presión del medio por encima y por debajo de su valor de equilibrio. Esta variación incremental se conoce como presión acústica (p).

Ondas Longitudinales y Transversales

Las ondas que requieren un medio elástico para su propagación se clasifican en longitudinales y transversales. En las ondas longitudinales, el desplazamiento de las partículas del medio vibratorio ocurre en la misma dirección que la propagación de la onda. Las ondas sonoras en el aire son longitudinales. En contraste, en las ondas transversales, la vibración de las partículas es perpendicular a la dirección de propagación (estas ondas solo se propagan en sólidos).

Propiedades Físicas de las Ondas Sonoras

Varias propiedades físicas son fundamentales para describir las ondas sonoras:

• Frecuencia (f): El número de ciclos completos de la onda que ocurren por segundo, medido en Hertz (Hz). El rango audible para los humanos se encuentra aproximadamente entre 20 Hz y 20.000 Hz.

• Período (T): El tiempo necesario para completar un ciclo de la onda, medido en segundos. Es el inverso de la frecuencia (T = 1 / f).

• Longitud de onda (λ): La distancia entre dos puntos correspondientes en ondas sucesivas, medida en metros. La longitud de onda está relacionada con la velocidad del sonido (c) y la frecuencia (λ=c/f). En el rango audible, varía desde unos 17 metros (para 20 Hz) hasta 17 milímetros (para 20.000 Hz).

• Intensidad sonora (I): La energía que atraviesa la unidad de superficie perpendicular a la dirección de propagación en la unidad de tiempo, medida en vatios por metro cuadrado (W/m²).

• Frente de onda: La superficie que conecta todos los puntos del medio que se encuentran en la misma fase de vibración. Para ondas planas longitudinales que se propagan en una sola dirección, los frentes de onda son planos perpendiculares a la dirección de propagación.

La propagación de una onda sonora a través de un medio se describe mediante la ecuación de onda, que se deriva de las leyes de la dinámica, la conservación de la masa y las propiedades del medio (como la ley de los gases). Las ecuaciones de onda simples a menudo no consideran la disipación de energía debido a la viscosidad o la conducción de calor.

Las propiedades de un gas que influyen en su comportamiento como medio acústico incluyen su densidad (ρ), presión (P), temperatura (T), calor específico, coeficiente de viscosidad, conductividad térmica y coeficiente de cambio de temperatura. La densidad del aire se puede aproximar por la siguiente expresión:

donde T es la temperatura absoluta en Kelvin y P es la presión barométrica en Pascales.

La Ecuación de Propagación de Ondas Planas

Consideremos una onda plana que se propaga a lo largo del eje X a través del aire, un medio que asumimos homogéneo, isótropo y perfectamente elástico.

Figura 1. Propagación de una perturbación en la dirección X.

La presión acústica instantánea (p) en un punto x en el tiempo t está dada por la solución de la ecuación de onda:

donde c es la velocidad del sonido en el aire. Esta velocidad depende de la temperatura:

siendo t la temperatura en grados Celsius. A 0°C, la velocidad del sonido es aproximadamente 331 m/s, y a 20°C es de unos 343 m/s.

Una función general que describe una onda que se propaga sin distorsión a lo largo del eje X es de la forma f (ct − x) para una onda que viaja en la dirección positiva de X, y f (ct + x) para una onda que viaja en la dirección negativa.

Las magnitudes fundamentales asociadas a una onda plana longitudinal de período T, velocidad de fase c y longitud de onda λ que se propaga en la dirección X son:

• Desplazamiento (ξ): El desplazamiento de las partículas desde su posición de equilibrio.

• Presión acústica (p): La variación de presión respecto a la presión de equilibrio.

• Condensación (s): El cambio relativo en la densidad del medio.

• Velocidad vibratoria de la partícula (v): La velocidad con la que vibran las partículas del medio.

Para ondas planas que se propagan en la dirección positiva de X, la presión acústica, la condensación y la velocidad vibratoria de la partícula están en fase, mientras que están desfasadas 90° con respecto al desplazamiento.

Energía e Intensidad de las Ondas Sonoras

Una onda sonora transporta energía desde la fuente a través del medio. Esta energía se manifiesta como energía cinética (debido al movimiento de las partículas) y energía potencial (asociada a la compresibilidad del fluido). La densidad de energía (e) es la energía por unidad de volumen transportada por la onda.

La intensidad acústica (I) se define como el valor medio del flujo de energía por unidad de área perpendicular a la dirección de propagación, medida en vatios por metro cuadrado (W/m²). Para ondas planas longitudinales, la intensidad está relacionada con la densidad de energía por:

donde c es la velocidad del sonido.

La relación entre la presión acústica (p) y la velocidad de la partícula (v) en un medio se define como la impedancia acústica específica (Z) del medio para ese tipo de onda:

Para ondas planas, la impedancia acústica específica tiene un valor:

La Escala de los Decibelios: Midiendo la Intensidad Sonora

Debido al amplio rango de intensidades sonoras que el oído humano puede percibir (desde 10⁻¹² W / m² hasta 10W / m²), y a la respuesta logarítmica del oído, se utiliza comúnmente una escala logarítmica para expresar los niveles sonoros: la escala de decibelios (dB).

El nivel de intensidad (LI) de una intensidad sonora I se define como:

donde Iref es la intensidad de referencia en el aire, que se toma como 10⁻¹² W / m², aproximadamente el umbral de audición a 1000 Hz.

Dado que la intensidad es proporcional al cuadrado de la presión acústica (I = p² / (ρ ⋅ c) para ondas planas), el nivel de presión sonora (Lp) se define como:

donde pref  es la presión acústica de referencia en el aire, que se toma como 2 ⋅ 10⁻⁵ N / m² (0.0002 microbares).

De manera similar, el nivel de potencia sonora (Lw) de una potencia sonora W es:

donde Wref  es la potencia de referencia, típicamente 10⁻¹² vatios.

Es crucial especificar la referencia utilizada al indicar un nivel en decibelios.

Suma de Niveles Sonoros

Para sumar dos o más niveles de presión sonora (L1, L2, ..., Ln), se deben convertir primero a intensidades, sumarlas y luego convertir el resultado nuevamente a nivel:

Existe un método gráfico simplificado para sumar dos niveles, basado en la diferencia entre ellos (Figura 2.).

Figura 2. Diagrama para sumar niveles en dB.

Medición del Nivel Sonoro de una Fuente en un Ambiente Ruidoso

Determinar el nivel sonoro real de una fuente (Ls) en un ambiente ruidoso con un nivel de ruido ambiental (Ln) requiere considerar el nivel total medido (Ls + n). Se utiliza un diagrama de corrección (Figura 3.) basado en la diferencia entre el nivel total y el nivel de ruido ambiental para estimar el nivel de la fuente. Si la diferencia es menor de 3 dB, la medición es imprecisa.

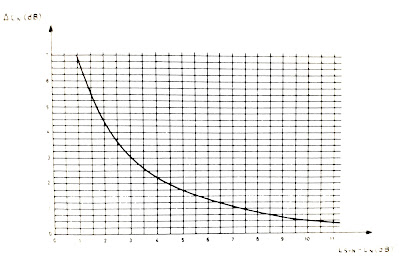Figura 3. Diagrama para determinar el nivel de presión sonora real de una fuente sonora, en un ambiente ruidoso.

Al estudiar la propagación de ondas y la impedancia acústica, se pueden establecer analogías con la propagación de corriente y la impedancia en circuitos eléctricos, así como con el movimiento de masas y la resistencia en sistemas mecánicos, como se exploró en entradas anteriores, ("Analogías de la Acústica con los Sistemas Eléctricos" y "Analogías de la Acústica con los Sistemas Mecánicos").

Conclusión:

Las ondas planas longitudinales son la base de cómo experimentamos el sonido en el aire. Su propagación, caracterizada por la frecuencia, la longitud de onda y la velocidad, genera variaciones de presión que nuestros oídos interpretan. La escala de decibelios nos proporciona una herramienta poderosa para cuantificar la intensidad y la presión de estas ondas, permitiéndonos comprender mejor el vasto mundo del sonido que nos rodea.