.jpg)
Desvelando el Secreto del Ancho de Banda Proporcional: Una Perspectiva Auditiva del Espectro
En el fascinante mundo del procesamiento de señales, especialmente en el ámbito del audio y la acústica, los filtros son herramientas esenciales para moldear el sonido y analizar su contenido frecuencial. Dentro de la diversa familia de filtros, los filtros de ancho de banda proporcional se distinguen por una característica fundamental: su ancho de banda varía directamente con la frecuencia central, manteniendo una relación constante entre la frecuencia superior e inferior de corte. Esta propiedad los hace intrínsecamente ligados a nuestra percepción auditiva, que también opera de manera aproximadamente logarítmica en términos de frecuencia.
La Definición Fundamental: Una Relación Constante
La premisa clave de los filtros de ancho de banda proporcional se expresa mediante la siguiente relación:
- f2 es la frecuencia superior de corte del filtro.
- f1 es la frecuencia inferior de corte del filtro.
Resoluciones Comunes: Octava y Tercio de Octava
La octava, un intervalo musical fundamental donde la frecuencia se duplica, sirve como base para definir resoluciones de filtro proporcionales estándar:
- Filtro de Octava: En este tipo de filtro, la relación entre la frecuencia superior e inferior de corte es:
- Filtro de Tercio de Octava: Este filtro divide la octava en tres partes iguales en una escala logarítmica, resultando en una relación de frecuencia:
De manera similar, existen filtros de media octava (f2 / f1 = 2½ ≈ 1.414), doceava de octava (f2 / f1 = 2⅟ 12 ≈ 1.059), y otras resoluciones.
 |
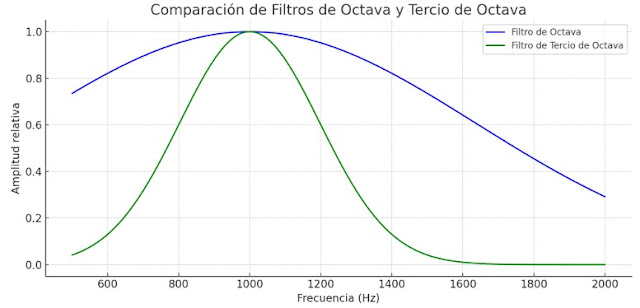| Figura 1: Representación gráfica del espectro de frecuencias mostrando filtros de ancho de banda proporcional de octava y tercio de octava centrados en la misma frecuencia. |
La Figura 1 ilustraría un gráfico del espectro de frecuencias con dos filtros de paso de banda centrados en la misma frecuencia. El filtro de octava mostraría un ancho de banda más amplio que el filtro de tercio de octava, enfatizando cómo una menor división de la octava resulta en una mayor selectividad (un ancho de banda más estrecho en relación con la frecuencia central).
La Variación del Ancho de Banda con la Frecuencia
La característica definitoria de los filtros de ancho de banda proporcional es que su ancho de banda absoluto (en Hertz) aumenta a medida que la frecuencia central del filtro se eleva, mientras que la proporción relativa del ancho de banda con respecto a la frecuencia central permanece constante.
Consideremos la Figura 1. con un filtro de tercio de octava:
- Relación de proporcionalidad:
Escenario 1: Frecuencia Central Alrededor de 100 Hz
Aunque la frecuencia central (fc) para un filtro de paso de banda se calcula geométricamente
, podemos usar la relación de proporcionalidad para encontrar f1 y f2 si asumimos que fc está aproximadamente en el centro logarítmico. Para simplificar la ilustración, usemos tus valores: f1 = 80Hz y f2 = 125Hz.
hay una pequeña discrepancia debido al redondeo y la aproximación de la frecuencia central).
- Ancho de banda (w) = f2 − f1 = 125Hz − 80Hz = 45Hz
Escenario 2: Frecuencia Central Alrededor de 200 Hz (una octava más arriba)
Manteniendo la misma relación de proporcionalidad (aproximadamente 1.26 para un tercio de octava), si la frecuencia central se duplica, el ancho de banda también se duplica aproximadamente. Usando tus valores: f1 = 160 Hz y f2 = 250Hz.
f = 1.56 (la proporción se mantiene).- Ancho de banda (w) = f2 − f1 = 250 Hz − 160 Hz = 90 Hz (el ancho de banda se ha duplicado).
Este ejemplo ilustra claramente cómo cada vez que subimos una octava en la frecuencia central, el ancho de banda del filtro proporcional se duplica.
 |
| Figura 2: Representación gráfica del espectro de frecuencias mostrando un filtro de tercio de octava centrado en 100 Hz y luego en 200 Hz, ilustrando el aumento del ancho de banda. |
La Figura 2 mostraría dos curvas de respuesta de filtro de tercio de octava. La curva centrada en 200 Hz sería más ancha (en Hz) que la curva centrada en 100 Hz, aunque ambas mantendrían una forma similar en una escala logarítmica.
Implicaciones Prácticas: Precisión en Bajas Frecuencias
Una consecuencia importante de la variación del ancho de banda con la frecuencia es que los filtros proporcionales ofrecen una mayor precisión (un ancho de banda absoluto más estrecho) en las frecuencias bajas en comparación con las frecuencias altas, para la misma resolución (por ejemplo, tercio de octava).
- A 100 Hz, un filtro de tercio de octava tiene un ancho de banda de aproximadamente 45 Hz.
- Si extrapolamos a 8 kHz (varias octavas por encima), el ancho de banda de un filtro de tercio de octava sería significativamente mayor: Aproximadamente 6.64 octavas entre 100 Hz y 8000 Hz (log2 (8000 / 100) ≈ 6.64). Por cada octava, el ancho de banda se duplica. Entonces, el ancho de banda a 8 kHz sería aproximadamente 45 Hz ⋅ 26.64 ≈ 3700Hz.
Esta característica de los filtros proporcionales se alinea con nuestra percepción auditiva, donde las diferencias de frecuencia en las regiones graves son más perceptibles en términos absolutos (en Hz) que en las regiones agudas.
Aplicaciones Comunes: Análisis y Ecualización Acústica y Musical
Los filtros proporcionales, con resoluciones de octava, tercio de octava y otras divisiones, son ampliamente utilizados en diversas aplicaciones:
- Analizadores de Espectro Acústico: Para analizar el contenido frecuencial de sonidos y ruidos en entornos acústicos, los analizadores suelen emplear filtros de tercio de octava (o incluso resoluciones más finas como doceava de octava) para obtener una representación del espectro que se asemeja a cómo el oído humano percibe las bandas de frecuencia.
- Ecualizadores Gráficos: Muchos ecualizadores gráficos dividen el espectro de audio en bandas que corresponden a fracciones de octava (típicamente octavas o tercios de octava). Esto proporciona a los usuarios un control intuitivo sobre el balance tonal del sonido, ya que las bandas se corresponden aproximadamente con las regiones de frecuencia que son perceptualmente significativas.
- Mediciones Acústicas: En mediciones de aislamiento acústico, tiempo de reverberación y otras propiedades acústicas de espacios, los filtros de octava y tercio de octava son estándares para analizar la respuesta del sistema en diferentes bandas de frecuencia relevantes para la audición humana.
- Procesamiento de Audio Musical: En la mezcla y masterización, los ecualizadores paramétricos y gráficos que ofrecen anchos de banda proporcionales permiten a los ingenieros esculpir el sonido de instrumentos y voces de manera musicalmente intuitiva.
 |
| Figura 3. EQ gráfico KlarkTeknik DN370 |
Conclusión: Una Perspectiva Auditiva del Filtraje
Los filtros de ancho de banda proporcional ofrecen una forma de analizar y manipular el espectro de frecuencias que se alinea de manera fundamental con la forma en que percibimos el sonido. Su característica de ancho de banda variable, que aumenta con la frecuencia central, los convierte en herramientas valiosas en campos tan diversos como la acústica arquitectónica, el análisis de ruido ambiental y la producción musical. Al proporcionar una resolución más fina en las bajas frecuencias, donde los cambios absolutos son más significativos para nuestra audición, los filtros proporcionales nos brindan una perspectiva "auditiva" del paisaje sonoro.
.jpg)
